
Reciban un cordial saludo, el motivo de la presente es para hacer llegar a ustedes las actividades y deberes del área de Matemáticas ha ser realizadas en casa mientras se encuentre en vigencia el periodo de cuarentena obligatoria debido a la emergencia sanitaria en nuestro país.
- Los ejercicios deben ser copiados en el cuaderno de materia en caso de que no tenga el libro de actividades.
- Los deberes semanales deben ser enviados todos los viernes mientras dure la suspensión de clases.
- Los cuadernos deben tener los margenes trazados color rojo (derecho e izquierdo).
- La letra debe ser obligatoriamente cursiva.
- Tomar en cuenta el orden y el aseo.
Agradeciendo la atención prestada me despido deseando bendiciones para sus hogares.
- Realizar la pág. 75 y 78 del libro de actividades.
Jueves 23 de Abril
especifico.
matematicas.
Ambas unidas nos ayudan a analizar las informaciones de los datos en hojas de
cálculos para ser representadas gráficamente por medio de tablas o diagramas .
Actividades:
1. Observa el vídeo sobre Estadísticas de excel y en tu libro de texto Talento matemático
trabaja con las páginas 73 - 74 para que siga los pasos y realices tu primera tabla de
estadísticas de excel.
2. Una vez realizada tu primera tabla de estadísticas de excel realiza las actividades de
las páginas 79-80
 |
| Agregar leyenda |
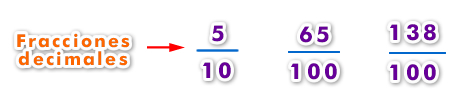



3- Transformación de decimal a fracción
Para escribir un número decimal en forma de fracción decimal, se escribe en el numerador el número decimal sin coma, y en el denominador la unidad seguida de tantos ceros como cifras decimales tiene el número decimal. La fracción obtenida se puede simplificar si lo deseas.
Por ejemplo:

Actividad:
Copiar en el cuaderno de materia solo los conceptos subrayados con color amarillo y según el concepto copiar 1 ejemplo.
Deber:
- Realizar la página 91 - 92
- Realizar la siguiente actividad


Se reconoce como números decimales a aquellos que cuentan con:
- Una parte entera, más
- Una parte decimal diferente a 0
Es decir que no alcanzan a componer un entero.
¿Cual es la relación de los decimales con las fracciones?
- La Unidad se representa por 1
- La Décima es la unidad dividida en 10 partes iguales = 1/10 = 0,1
- La Centésima es la unidad dividida en 100 partes iguales = 1/100 = 0,01
- La Milésima es la unidad dividida en 1000 partes iguales = 1/1000 = 0,001
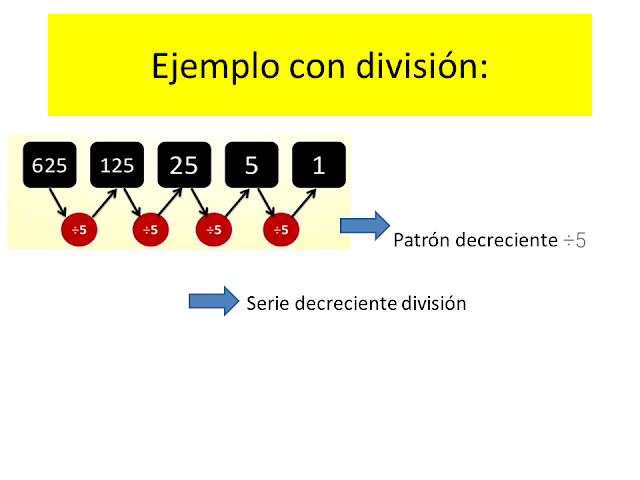
Divisiones con decimales en el cociente
Si en una división el dividendo es menor que el divisor el cociente tendrá decimales.
Vamos a ver con un ejemplo cómo se hace esta división.
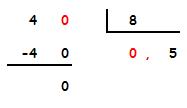
El dividendo (4) es menor que el divisor (8).
Para poder realizar la división pondremos un 0 en el dividendo y otro 0 en el cociente seguido de coma.
Ahora seguimos como en una división normal:
ejemplo:
Ponemos un 0 en el dividendo y un 0 en el cociente seguido de coma.
Seguimos como en una división normal:
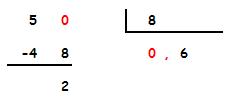
Vamos a ver una peculiaridad de estas divisiones:
Al no ser una división exacta, el resto es 2, podemos ponerle un 0 a su derecha y seguir dividiendo.
Y en los sucesivos restos, mientras no sean 0, podemos seguir operando de esta manera, añadiendo cifras decimales al cociente.
Dividir un número decimal por 10, 100, 1.000
Por ejemplo:
32,7 : 10
124,6 : 1.000
14,81 : 1.000
Para calcular el resultado:
a) Primero escribimos en el resultado el dividendo.
b) Luego en el resultado desplazaremos la coma hacia la izquierda tantas posiciones como ceros lleve el divisor.
ejemplos:
a) 32,7 : 10
Primeros escribimos en el resultado el dividendo.
32,7 : 10 = 32,7
Luego desplazaremos la coma hacia la izquierda una posición ya que hemos dividido por 10 que lleva 1 cero:
32,7 : 10 = 3,27
b) 124,6 : 1.000
Primeros escribimos en el resultado el dividendo.
124,6 : 1.000 = 124,6
Luego desplazaremos la coma hacia la izquierda tres posiciones ya que hemos dividido por 1.000 que lleva 3 ceros:
124,6 : 100 = ,1246
Cuando la coma queda al principio de un número significa que ese número no tiene parte entera. Por eso delante de la coma se pone un 0:
124,6 : 100 = 0,1246
Puede ocurrir que en el divisor haya más ceros que cifras enteras en el dividendo, por lo que no podemos desplazar hacia la izquierda la coma tantas posiciones como ceros, ¿qué hacemos? Las posiciones que no podamos desplazar la coma la completaremos con ceros:
ejemplo:
a) 14,81 x 1.000
Primeros escribimos en el resultado el dividendo.
14,81 : 1.000 = 14,81
Luego desplazaremos la coma hacia la izquierda tres posiciones ya que hemos dividido por 1.000 que lleva 3 ceros:
Como 14,81 tan sólo tiene dos cifras enteras tan sólo podemos desplazar la coma hacia la izquierda 2 posiciones, por lo que completaremos el movimiento que nos falta poniendo 1 cero delante:
14,81 : 1.000 = ,01481
Y como vimos antes, delante de la coma se pone otro 0:
14,81 : 1.000 = 0,01481

Sistema de coordenadas rectangulares
¿Cómo
funcionan las coordenadas cartesianas?
Si queremos localizar algo en un plano necesitamos:
· Una medida horizontal: izquierda-derecha. A la que llamaremos X.
Una medida vertical: arriba-abajo. A la que llamaremos Y.
Ejemplo:
También tenemos una dirección vertical,
arriba-abajo. Igual que en el eje X, los valores empiezan en el origen con cero
y van creciendo a medida que nos desplazamos hacia arriba. Éste es el eje Y de coordenadas.
el primer número indica cuánto a la derecha se
encuentra y el segundo cómo de arriba está. Normalmente estos números van
separados por una coma y rodeados por paréntesis de la siguiente manera: (X,Y).
Números naturales de hasta seis cifras
Son aquellos que nos ayudan a saber que cantidad hay en un conjunto de
cosas; no solo para su contabilización sino también para ordenarlos y son
infinitos.
Los números naturales son el: 1, 2, 3, 4, 5, 6, 7,
8, 9… etc.
Para leer un número de 6 cifras,
se divide el número con puntos en grupos de tres, empezando por la derecha.
Después se lee el número formado en cada grupo empezando por la izquierda y
cuando se llegue al punto se dice mil.
Ejemplo:
523658
⇒
Primero dividimos el número ⇒ 523.658
El
número que queremos leer es el quinientos veintitrés mil seiscientos cincuenta
y ocho.
Descomposición de números naturales
Para descomponer un número natural
se debe realizar de forma aditiva según el valor posicional de cada cifra.
Ejemplo:
![]()
![]()
![]()
7![]()
![]() 90
90
![]() 800
800
![]() 5.000
5.000
![]() 30.000
30.000
![]() 600.000
600.000
635.897
Deber:


1- ¿ Qué es una multiplicación ?
La multiplicación es una suma abreviada de sumando iguales.
Ejemplo:
2+2+2+2+2= 10 Es igual 5 x 2 = 10
2- Términos de la multiplicación.

Conmutativa: el orden de los factores no altera el producto.
2 x 3 = 3 x 2
6 = 6
Asociativa: en una multiplicación de 3 o más factores se puede empezar multiplicando los 2 primeros y el resultado multiplicarlo por el tercero; o empezar multiplicando el segundo por el tercero y el resultado multiplicarlo por el primero.
(4 x 4) x 5 = 4 x (4 x 5)
16 x 5 = 4 x 20
80 = 80
Propiedad modulativa: la multiplicación tiene un elemento neutro que es el 1. Si se multiplica cualquier número por 1 el resultado es el mismo número:
9 x 1 = 9
Propiedad distributiva: cuando se multiplica un número por una suma (resta) se puede:
- Resolver primero la suma (resta) y el resultado multiplicarlo por el número .
- O multiplicar el número por cada uno de los elementos de la suma (resta) y luego sumar (restar) los resultados.
Ejemplos:
a) 3 x (4 + 7) = 3 x 4 + 3 x 7
b) 2 x (5 - 3) = 2 x 5 - 2 x 3
















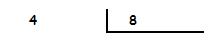
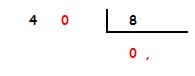
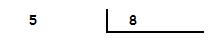
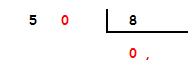
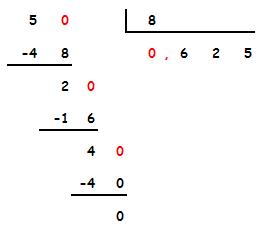









No hay comentarios.:
Publicar un comentario